For the past few years I’ve been reading about this new language called rust. When it first came out in 2010, I had taken it for a spin and found that “fighting the borrow checker” was very time consuming with unintelligible error messages generated by the compiler. Since then I never really went back to […]
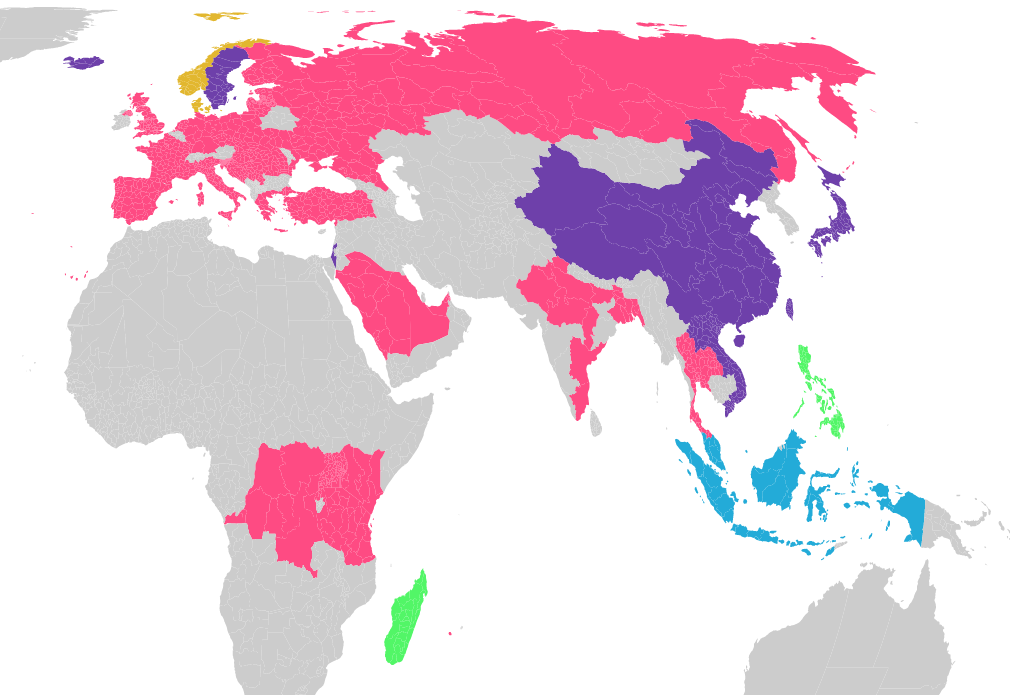
TL; DR — Many languages have a lot of similar words. These similarities often times relate to similarities arising due to trade, empires and human migrations. I built an open source tool to automatically detect and visualize their similarities. The tool is in its infancy — its not perfect. Having grown up in a multicultural […]
Raspberry Pis have become a rage wherever one needs to add some electronics to a project, yet they are not a very good tool for controlling electronics. It comes with few 3v3 digital GPIO pins. Now say for instance you want to hook on a potentiometer to the Pi how would you do it? The […]
Python Asyncio tutorial
Note: This tutorial only works beyond python 3.5.3 Python has always been known as a slow language with poor concurrency primitives. Yet no one can deny that python is one of the most well thought out languages. Prototyping in python is way faster than most languages and the rich community and libraries that have grown […]
I have successfully used HoG for a number of object recognition tasks. In fact I have found it to be a ridiculously good image descriptor particularly for rigid bodies. It can easily differentiate between various objects given very few training samples and is much faster than any of the existing object detection algorithms. While I […]

When you look around the market, there are many different types of 3D scanners and 3D sensors out there. A quick look at PCL’s IO library lists a number of different sensors out there. Microsoft has their Kinect which use Time Of Flight to measure depth. The PR2 robot uses projected stereo mapping (i.e. It […]
In order to take into account the varying complexities of vocabulary used we looked at offline algorithms for skewness. Now I propose a simpler method. Skewness requires a very large number of multiplications and divisions to be performed. This makes it unsuitable for quick calculations on an AVR as the AVR architecture used by an […]
Regarding µSpeech 4.1.2+
Dear Users of µSpeech library, With the release of the 4.2.alpha library I have been reciveing a lot of mail as to how the debug µSpeech program does not work. I sincerely, apologize for this inconvenience as I have very little time on hand to address the issues associated with 4.1.2+ and 4.2.alpha. I realized that […]
Ok, so making rovers with one Arduino is so overdone. What if you had two rovers that worked together to solve problems. Or even turn. This can be fairly challenging. In order to achieve communication between to Arduino’s, one can use the two wire interface, known as I2C. I2C is a method of communicating between […]
In this page we shall begin to program our robot. To understand how to program we first need to know how a computer works. A computer understands nothing. It is up to the programmer to tell it what to do. At the heart of the computer is a CPU. The CPU translates a piece of […]